How Far is a Degree?
You're familiar with latitude, longitude, degrees, minutes, and seconds. But do you know the ground distance of one degree of arc? How about one minute of arc - how long is that? One second of arc? When dealing with latitude and longitude coordinates, it is often helpful to have a general idea of the ground distance covered by various arc lengths.
You learned in the previous topic that the Earth is not a perfect sphere, but is in fact an ellipsoid. To determine the ground distance of various arc lengths for an ellipse, we have to calculate the perimeter of an ellipse. This is found by the following formula*, where a is the equatorial radius (aka, semi-major axis) and b is the polar radius (aka, semi-minor axis):
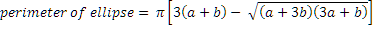
The table below shows the ground distance covered by various great circle arc lengths along the longitudinal meridians (a longitudinal great circle follows a line of longitude from the North Pole to the equator to the South Pole, then north to the equator and back to the starting point at the North Pole - for example: starting at the North Pole along the 0° meridian, then following the 0° meridian south to the South Pole, then north following the 180° meridian back to the starting point at the North Pole).
|
|
Meters |
Feet |
|
WGS84 equatorial radius (a) |
6,378,137.00 |
20,925,646.33 |
|
WGS84 polar radius (b) |
6,356,752.30 |
20,855,486.55 |
|
|
|
|
|
WGS84 average radius |
6,367,444.65 |
20,890,566.44 |
|
|
|
|
|
circumference of a circle = (2)(pi)(radius) |
40,007,834.67 |
131,259,300.10 |
|
perimeter of WGS84 ellipse * |
40,007,862.87 |
131,259,392.63 |
|
|
|
|
|
360° = |
40,007,862.87 |
131,259,392.63 |
|
|
|
|
|
1 degree = |
111,132.95 |
364,609.42 |
|
0.1 degree = |
11,113.30 |
36,460.94 |
|
0.01 degree = |
1,111.33 |
3,646.09 |
|
0.001 degree = |
111.13 |
364.61 |
|
0.000,1 degree = |
11.11 |
36.46 |
|
0.000,01 degree = |
1.11 |
3.65 |
|
0.000,001 degree = |
0.11 |
0.36 |
|
|
|
|
|
1 minute = |
1,852.22 |
6,076.82 |
|
0.1 minute = |
185.22 |
607.68 |
|
0.01 minute = |
18.52 |
60.77 |
|
0.001 minute = |
1.85 |
6.08 |
|
0.000,1 minute = |
0.19 |
0.61 |
|
|
|
|
|
1 second = |
30.87 |
101.28 |
|
0.1 second = |
3.09 |
10.13 |
|
0.01 second = |
0.31 |
1.01 |
|
0.001 second = |
0.03 |
0.10 |
|
|
|
|
|
0.001 second = |
0.03 |
0.10 |
|
0.000,001 degree = |
0.11 |
0.36 |
|
0.000,1 minute = |
0.19 |
0.61 |
|
0.01 second = |
0.31 |
1.01 |
|
0.000,01 degree = |
1.11 |
3.65 |
|
0.001 minute = |
1.85 |
6.08 |
|
0.1 second = |
3.09 |
10.13 |
|
0.000,1 degree = |
11.11 |
36.46 |
|
0.01 minute = |
18.52 |
60.77 |
|
1 second = |
30.87 |
101.28 |
|
0.001 degree = |
111.13 |
364.61 |
|
0.1 minute = |
185.22 |
607.68 |
|
0.01 degree = |
1,111.33 |
3,646.09 |
|
1 minute = |
1,852.22 |
6,076.82 |
|
0.1 degree = |
11,113.30 |
36,460.94 |
|
1 degree = |
111,132.95 |
364,609.42 |
Arc lengths and their corresponding longitudinal great circle ground distances for the WGS84 ellipsoid
* The formula to approximate the perimeter of an ellipse was obtained from http://mathworld.wolfram.com/Ellipse.html#eqn70
The Region 7 Land Mapper was developed, and is maintained by, the U.S. Fish & Wildlife Service, Region 7, Division of Realty. Questions, comments,and suggestions should be directed to ak_realty@fws.gov
This page was last updated: Thursday, March 13, 2025