A Geodesy Primer
Geodesy is the science of measuring and monitoring the size and shape of the Earth. Although it is a field of science that most people never encounter in an academic sense, it is one which affects everyone in a practical sense. Without geodesy...
|
•We could not figure out precisely where we are •Accurate maps would be impossible to make •GPS navigation would lead you astray •...and other horrible stuff |
The ability to accurately determine locations on the surface of the Earth is fundamental to GIS and GPS, and this is accomplished by using various datums, map projections, and coordinate systems. When working with the Land Mapper, or any geographic data, it is essential to have a basic understanding of these concepts.
The discussion below will give you a basic understanding of essential geodesy concepts. To learn more, refer to the ArcGIS Help Library.
Datum - What is it?
Simply put, a datum is a set of numbers that define the shape, size, and position of an ellipsoid which best approximates the true surface of the Earth, either locally or globally.
Ok, what's an ellipsoid?
Consider a bowling ball. It is a sphere. That is, its equatorial radius of 4.25" is the same as its polar radius. If you could spin a bowling ball so fast that centrifugal force were able to deform the ball, its equatorial radius would be slightly larger than 4.25" and its polar radius would be slightly less than 4.25". The result would be a sphere that appears to be squashed, similar to what would happen to a round balloon if you squeezed it from both sides simultaneously. This flattened shape is called an oblate spheroid (basically, a three-dimensional ellipse). The example of the deformation of the spinning bowling ball is exactly what happens to the Earth - its rotation about the polar axis causes an equatorial bulge, with a resultant flattening at the poles.

The Earth represented as an oblate spheroid
(scale is greatly exaggerated)
So, what is the "set of numbers that define the size, shape, and position of the ellipsoid"?
An ellipsoid can be mathematically described by four parameters: semi-major axis (the equatorial radius), semi-minor axis (the polar radius), the degree of flattening, and the ellipsoid's position with respect to the center of the Earth. For example, here are the parameters for several datums that are commonly used in the United States:
|
Datum |
NAD27 |
NAD83 |
WGS84 |
|
Ellipsoid name |
Clarke 1866 |
GRS 1980 |
WGS 1984 |
|
Semi-major axis (meters) |
6,378,206.400 |
6,378,137.000 |
6,378,137.000 |
|
Semi-minor axis (meters) |
6,356,583.800 |
6,356,752.314 |
6,356,752.314 |
|
Inverse flattening |
0.00339008 |
0.00335281 |
0.00335281 |
|
Eccentricity squared |
0.00676866 |
0.00669438 |
0.00669438 |
|
Datum type |
Local (N. America) |
Local (N. America) |
Global |
You can see that there are slight differences in the values (indicated by bold type). The position of the ellipsoid with respect to the center of the Earth (indicated by the eccentricity) also varies among datums. The Clarke 1866 and GRS 1980 ellipsoids are positioned such that the surface of the ellipsoid better matches the North American continent. These are local datums, because they are optimized for use only in a certain part of the world. Conversely, the ellipsoids of global datums such as WGS84 are positioned to be closer to the center of the Earth, which gives the best approximation of the Earth's surface on a global scale.
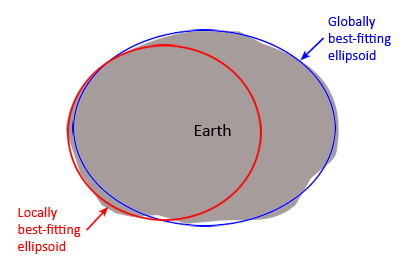
Illustration of the differences between local and global datums. The ellipsoid for a global datum
is sized and positioned to best represent the surface of the Earth on a global scale. Local datums
have their ellipsoids sized and positioned to better match a particular region of the Earth.
So the ellipsoids are different. Why does this matter?
All geographic coordinates (latitude and longitude) are derived from an ellipsoid. And since the ellipsoids have different numerical values, a latitude and longitude value for a particular datum will not have the same value in a different datum. Consider the following example:
|
Datum |
NAD27 |
NAD83 |
WGS84 |
|
Longitude |
134° 21' 49.21" |
134° 21' 55.59" |
134° 21' 55.66" |
|
Latitude |
58° 22' 3.30" |
58° 22' 2.13" |
58° 22' 2.15" |
All three coordinates above identify the same physical point on the Earth's surface, but the seconds value varies. This is due to the different ellipsoids associated with the datums. The reason why this matters is because if you don't know what datum your data is in, you or someone else will have to guess which datum the data are in, and this greatly increases the probability of positional errors when you import your data into the Land Mapper or GIS.
Map Projection - What is it?
A map projection is simply a method for converting, or projecting, the three-dimensional surface of the Earth onto a two-dimensional plane (for example, a piece of paper or a computer monitor) for the purpose of making a map and/or performing distance, direction, and area computations. There are numerous projections, each optimized for a particular purpose. For example, the Mercator projection is best used for marine navigation, because directions are correct, while other qualities such as area are distorted. Conversely, the Mollweide projection gives accurate areas, while directions are distorted. The examples below illustrate the differences between these two projections.
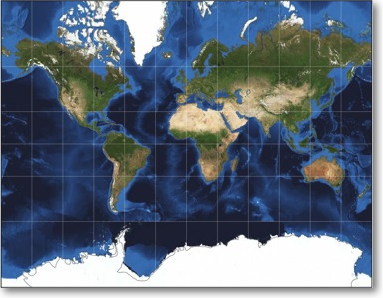
Mercator projection. Directions are
accurate, but area is greatly distorted
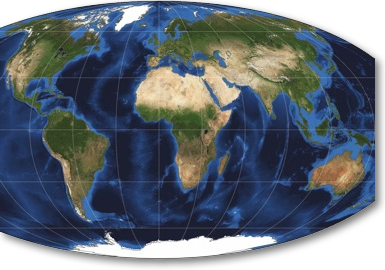
Mollweide projection. Areas are
accurate, but direction is distorted
Coordinate System - What is it?
A coordinate system is a way to describe positions on the surface of the Earth. The coordinates of a point can be expressed in several ways - as latitude and longitude, or as meters or feet. Latitude and longitude coordinates are used to express points within a geographic coordinate system, such as NAD27 or WGS84. Meters or feet are used with projected coordinate systems, such as Alaska Albers Equal Area Conic.
The $64,000 Question - Why do I need to know all this stuff?
The simple answer: if you don't know what datum and projection your data are referenced to, there's a very high probability that your data will not align correctly with other features when viewed in the Land Mapper or GIS. If you, as the owner of your data, don't know what datum it is referenced to, others who try to use it will have to guess, with likely incorrect results.
The Bottom Line - How to Properly Reference Geographic Coordinates
When documenting your data or when giving coordinates to others, you should always cite the datum and projection of the data. For example:
|
Datum |
Projection |
Coordinate |
|
|
NAD27 |
Geographic |
134° 21' 49.21" West |
58° 22' 3.30" North |
|
WGS84 |
Geographic |
134° 21' 55.66" West |
58° 22' 2.15" North |
|
NAD83 |
Alaska Albers Conic |
125,000 meters Easting |
2,570,000 meters Northing |
|
|
In the examples above, a point on the Earth is noted as an XY coordinate. X and Y refer to locations within a Cartesian coordinate system, where X identifies a position along the horizontal (X) axis and Y identifies a position along the vertical (Y) axis. •In a geographic coordinate system, longitude is expressed by the X value, and latitude is expressed by the Y value. •In a projected coordinate system, Easting is expressed by the X value, and Northing is expressed by the Y value. ...and Know Your Signs With geographic coordinate systems, it is critically important to understand how north, south, east, and west are represented by the coordinate values. Algebraic signs, plus (+) and minus (-) are used to indicate the compass directions, as such: •North latitude is represented as a positive value (+) •South latitude is represented as a negative value (-) •East longitude is represented as a positive value (+) •West longitude is represented as a negative value (-) |
|
|
Converting between latitude and longitude formats Latitudes and longitudes can be expressed in several different formats, such as: •45° 24' 13.4" (Degrees, minutes, seconds) •45° 24.223 (Degrees and decimal minutes) •45.40372222° (Decimal degrees) All three examples above are equivalent, that is, they identify the same spot on the Earth. You may run into situations where you must provide latitude and longitude values in a particular format. For example, you might have a lat/long coordinate in degrees, minutes, and seconds format, but the program you're working with might require you to input the lat/long in decimal degrees format. To do this, you have to convert from one format to another. You can do this using an online lat/long converter. There are many such converters available online, but here's one that's very easy to use: http://rumkin.com/tools/gps/degrees.php This site converts from any of the three formats to any of the other three. |
|
|
Latitude + Longitude + Datum = A Complete Coordinate, aka LLD = Problem Free! Casual use of latitude and longitude positions generally doesn't involve referencing the datum to which the lat/long is tied. However, when dealing with GIS a higher level of precision is required, thus lat/long values must always include the associated datum. When noting lat/long coordinates or giving lat/long coordinates to someone, you must always report the datum which is used by the coordinates. Without the datum information, the user will have to guess which datum your lat/long coordinates are in, and this often leads to misalignment of features. Following are several examples of the correct way to note lat/long coordinates: •45.50, -150.25, NAD27 •45.50 N, 150.25 W, NAD83 •45° 30' 00" N, 150° 15' 00" W, WGS84 Note that for each example, the datum has been specified. A lat/long coordinate should never leave your desk without a datum specified. Remember: LLD = Problem Free! |
The Region 7 Land Mapper was developed, and is maintained by, the U.S. Fish & Wildlife Service, Region 7, Division of Realty. Questions, comments,and suggestions should be directed to ak_realty@fws.gov
This page was last updated: Thursday, March 13, 2025